一句话总结

南洋理工大学与复旦大学研究者提出无误差线性注意力（Error-Free Linear Attention, EFLA），通过利用秩-1矩阵性质推导连续时间动力学的精确闭式解，消除线性注意力中的离散化误差，在保持线性时间复杂度的同时避免误差累积，在噪声环境、更低困惑度及基准测试中均优于DeltaNet且无需额外参数。

核心贡献

• 揭示现有线性注意力方法因对连续时间动力学进行低阶离散化而产生数值不稳定性，尤其在长上下文场景中欧拉近似失效会导致截断误差，这解释了噪声环境与长序列中性能下降的原因。
• 将线性注意力重构为由一阶常微分方程（ODE）控制的连续时间动力系统，揭示标准实现对应欧拉离散化等次优数值积分方案，该理论视角建立了注意力机制与连续时间系统建模的桥梁。
• 推导出消除离散化误差的秩-1动力学矩阵精确闭式解，在保持线性时间复杂度的同时，通过语言建模困惑度提升及下游基准测试性能（优于DeltaNet且无额外参数）得到验证。

引言

长上下文建模对高效处理语言理解等场景中的长序列至关重要，而标准注意力机制因二次复杂度在大规模应用中面临计算瓶颈。现有方法（如线性注意力）常因连续动力学的近似离散化引发数值不稳定性，导致性能下降。作者通过证明：当从连续时间公式推导时，秩-1线性注意力存在精确无误差的离散化解，为增强现有线性注意力实现的可靠性提供了严谨理论基础（无需新架构组件）。该洞见为构建更稳定的长上下文模型开辟路径，同时可与RetNet或Hyena等替代线性时间框架互补。

方法

作者采用连续时间动力系统视角，将线性注意力重构为一阶常微分方程（ODE）的精确无误差解。不同于依赖欧拉或龙格-库塔等低阶数值近似，他们推导出捕获注意力状态连续演化的闭式解析解，避免截断误差。通过利用底层动力学矩阵的秩-1结构，该解在保持数学保真度的同时实现线性时间复杂度。

核心公式始于将DeltaNet更新（通过梯度下降最小化重构损失）解释为连续时间ODE的离散化：

$$\frac{d\mathbf{S}(t)}{dt} = -\mathbf{A}_t \mathbf{S}(t) + \mathbf{b}_t,$$dtdS(t)​=−At​S(t)+bt​,

其中 $\mathbf{A}_t = \mathbf{k}_t \mathbf{k}_t^\top$At​=kt​kt⊤​ 且 $\mathbf{b}_t = \mathbf{k}_t \mathbf{v}_t^\top$bt​=kt​vt⊤​。在离散输入序列的零阶保持假设下，该ODE控制状态矩阵 $\mathbf{S}(t)$S(t) 的演化（随时间累积键值关联）。标准线性注意力方法对应此系统的一阶欧拉积分，引入 $\mathcal{O}(\beta_t^2)$O(βt2​) 局部截断误差，并在刚性动力学下不稳定。

为消除误差，作者通过对龙格-库塔族取无穷阶极限推导ODE精确解：

$$\mathbf{S}_t = e^{ {-\beta_t\mathbf{A}_t} } \mathbf{S}_{t-1} + \int_0^{\beta_t} e^{ {-(\beta_t - \tau)\mathbf{A}_t} } \mathbf{b}_t \, d\tau.$$St​=e−βt​At​St−1​+∫0βt​​e−(βt​−τ)At​bt​dτ.

尽管矩阵指数通常带来 $\mathcal{O}(d^3)$O(d3) 计算成本，但 $\mathbf{A}_t$At​ 的秩-1特性允许闭式简化：对 $n \geq 1$n≥1 有 $\mathbf{A}_t^n = \lambda_t^{n-1} \mathbf{A}_t$Atn​=λtn−1​At​（其中 $\lambda_t = \mathbf{k}_t^\top \mathbf{k}_t$λt​=kt⊤​kt​），使指数项简化为：

$$e^{ {-\beta_t\lambda_t} } = \mathbf{I} - \frac{1 - e^{ {-\beta_t\lambda_t} } }{\lambda_t} \mathbf{A}_t.$$e−βt​λt​=I−λt​1−e−βt​λt​​At​.

类似地，由 $\mathbf{A}_t \mathbf{b}_t = \lambda_t \mathbf{b}_t$At​bt​=λt​bt​ 可简化积分项：

$$\int_0^{\beta_t} e^{ {-(\beta_t - \tau)\mathbf{A}_t} } \mathbf{b}_t \, d\tau = \frac{1 - e^{ {-\beta_t\lambda_t} } }{\lambda_t} \mathbf{b}_t.$$∫0βt​​e−(βt​−τ)At​bt​dτ=λt​1−e−βt​λt​​bt​.

整合后得到最终无误差线性注意力（EFLA）更新规则：

$$\mathbf{S}_t = \left( \mathbf{I} - \frac{1 - e^{ {-\beta_t\lambda_t} } }{\lambda_t} \mathbf{k}_t \mathbf{k}_t^\top \right) \mathbf{S}_{t-1} + \frac{1 - e^{ {-\beta_t\lambda_t} } }{\lambda_t} \mathbf{k}_t \mathbf{v}_t^\top.$$St​=(I−λt​1−e−βt​λt​​kt​kt⊤​)St−1​+λt​1−e−βt​λt​​kt​vt⊤​.

该更新保留与DeltaNet相同的代数结构，可无缝采用现有硬件高效并行技术。作者进一步通过展开递推关系推导块并行公式，将状态表示为衰减算子与累积输入的乘积，实现序列块的高效批处理计算，在保持 $\mathcal{O}(Ld^2)$O(Ld2) 复杂度的同时支持完全并行。

$\mathbf{A}_t$At​ 的谱特性还揭示隐式门控机制：键范数 $\lambda_t$λt​ 控制沿 $\mathbf{k}_t$kt​ 方向的衰减速率。大 $\lambda_t$λt​ 引发快速遗忘，小 $\lambda_t$λt​ 导致近线性衰减，有效优先保留历史上下文。当 $\lambda_t \to 0$λt​→0 时，EFLA恢复delta规则，证实先前线性注意力方法仅为非刚性动力学下的低阶近似。

通过将注意力机制扎根于连续时间动力学并推导其精确解，EFLA消除了离散化近似固有的数值误差，为现有线性注意力公式提供了理论严谨、可扩展且稳定的替代方案.

实验

• sMNIST数值稳定性测试：在像素丢弃、OOD强度缩放及高斯噪声下，EFLA（学习率3e-3）显著优于DeltaNet，验证其对误差累积与状态爆炸的鲁棒性.
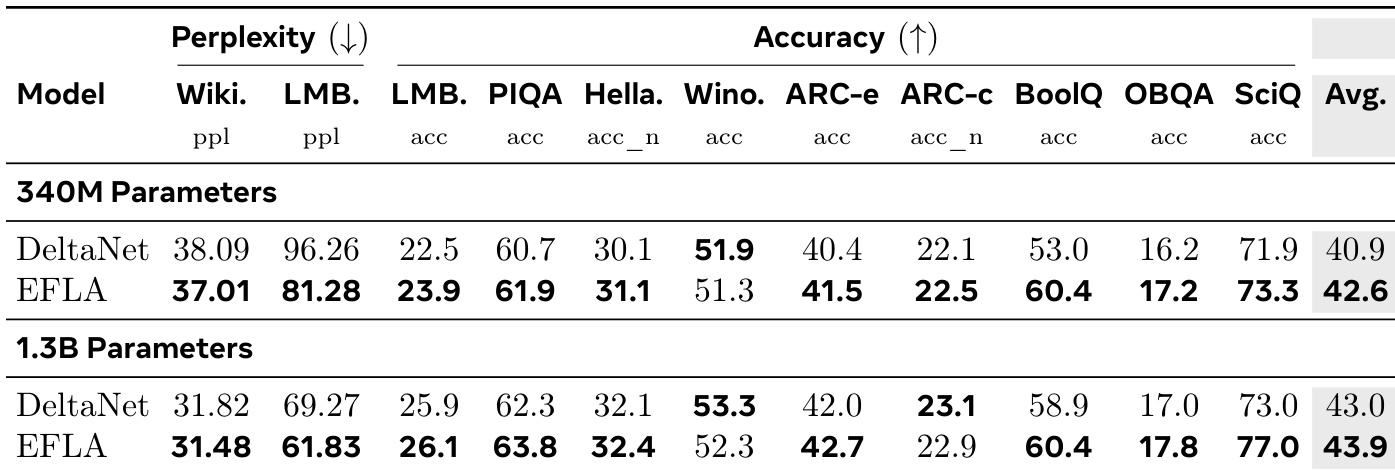
• Wikitext与LAMBADA语言建模：EFLA困惑度81.28（DeltaNet为96.26），LAMBADA准确率23.9%，BoolQ任务绝对准确率领先DeltaNet +7.4%，证实长序列信息保真度优势.
• 学习率分析：EFLA需更大学习率（3e-3）以抵消饱和效应，干扰测试中相比保守学习率（1e-4）展现出更优鲁棒性.

作者在340M与1.3B参数模型上对比EFLA与DeltaNet的语言建模及推理任务.结果显示EFLA在多数基准测试中持续领先：Wikitext与LAMBADA困惑度更低，BoolQ与SciQ等任务准确率更高，且模型规模扩大时性能差距进一步拉大.该提升归因于EFLA的精确衰减机制，其比DeltaNet的欧拉近似更有效保持长程上下文保真度.