一句话总结

作者提出了一种基于格拉斯曼流的新型无注意力序列模型，利用Gr(2, r)上的低秩子空间动态和普吕克嵌入，实现几何化的、线性可扩展的信息融合——在语言建模和自然推理任务上达到具有竞争力的性能，同时为密集自注意力提供了一种更具解析可处理性的替代方案。

主要贡献

• 本文挑战了“密集或近似自注意力对强大语言建模至关重要”的假设，将注意力重新诠释为一种高维张量提升操作，因其在层与头之间分析上的不可处理性而掩盖了模型行为。

• 提出一种基于格拉斯曼流的新型无注意力架构，其中局部词元对被建模为格拉斯曼流形Gr(2, r)上的二维子空间，通过普吕克坐标嵌入，并经由门控混合模块融合，实现隐藏状态的几何演化，无需显式成对权重。

• 在Wikitext-2和SNLI上进行评估，基于格拉斯曼的模型表现具有竞争力——困惑度比Transformer基线低10–15%，分类准确率略优，且在固定秩下序列长度复杂度为线性，与自注意力的二次代价形成鲜明对比。

引言

作者挑战了自注意力在序列建模中的基础性作用，该机制因表达能力强且可并行化，已成为Transformer的默认机制。尽管先前工作聚焦于优化注意力——通过稀疏化、近似或内存增强降低其二次复杂度——但这些方法仍需计算或近似一个$L \times L$L×L的注意力矩阵。其关键局限在于，注意力被视为不可或缺，尽管它只是实现表示几何提升的一种方式。作者提出格拉斯曼流作为根本不同的替代方案：不依赖注意力的成对交互，而是通过格拉斯曼流形上子空间的演化来建模序列动态，使用普吕克坐标编码几何关系。该方法完全消除了显式注意力的需求，提供了一种由几何驱动的序列建模机制，兼具数学严谨性与计算高效性。其主要贡献在于将这一格拉斯曼–普吕克流程集成到类似Transformer的架构中，证明几何混合可替代注意力，同时保持强大性能，并为未来引入全局不变量等扩展提供了可能。

数据集

• 使用的数据集为Wikitext-2-raw，是语言建模任务中广泛采用的基准。
• 文本序列通过将原始文本划分为固定长度的连续块生成，块大小为128或256个词元。
• 采用近似30,522个词元的WordPiece风格词汇表，与BERT式分词一致。
• 作者比较了两种模型架构：TransformerLM（标准的仅解码器Transformer）和GrassmannLM（将每个自注意力块替换为因果格拉斯曼混合块）。
• 评估两种模型深度：浅层（6层）和深层（12层），两种模型均保持相同的嵌入维度（d=256）、前馈维度（d_ff=1024）和4个注意力头。
• 对GrassmannLM，使用降低的维度r=32，并应用多尺度窗口模式：6层模型为{1, 2, 4, 8, 12, 16}，12层模型为重复模式（1, 1, 2, 2, 4, 4, 8, 8, 12, 12, 16, 16）。
• 两种模型均使用相同的优化器和学习率调度进行30轮训练，仅在混合块类型上不同。
• 报告训练过程中最佳验证困惑度，批量大小为32（L=128）和16（L=256）。

方法

作者利用对自注意力的几何重解释，提出一种替代序列建模框架，用基于格拉斯曼流的结构化、无注意力过程取代标准注意力机制。该方法通过从无结构张量提升转向有限维流形上的受控几何演化，重新思考序列模型的核心交互机制。整体架构称为因果格拉斯曼Transformer，遵循Transformer编码器的一般结构，但将每个自注意力块替换为因果格拉斯曼混合层。该层通过降低词元表示的维度，将局部成对交互编码为格拉斯曼流形上的几何子空间，并通过门控机制将结果特征融合回隐藏状态空间。

过程始于词元和位置嵌入，输入词元通过学习的嵌入矩阵映射到$d$d维空间，并附加位置编码。此初始隐藏状态序列随后通过$N$N个堆叠的因果格拉斯曼混合层处理。每一层执行一系列操作，旨在捕捉局部几何结构，而无需依赖显式成对注意力权重。首先，线性降维步骤通过$z_t = W_{\text{red}} h_t + b_{\text{red}}$zt​=Wred​ht​+bred​将每个隐藏状态$h_t \in \mathbb{R}^d$ht​∈Rd投影到低维空间，得到$Z \in \mathbb{R}^{L \times r}$Z∈RL×r，其中$r \ll d$r≪d。该降维步骤在压缩表示的同时保留关键局部信息。

如图所示，框架接下来为一组多尺度窗口大小$\mathcal{W}$W（如$\{1, 2, 4, 8, 12, 16\}${1,2,4,8,12,16}）构建缩减状态的局部对$(z_t, z_{t+\Delta})$(zt​,zt+Δ​)，通过仅将每个位置$t$t与未来位置配对来保证因果性。对于每一对，作者将两个向量的张成解释为$\mathbb{R}^r$Rr中的二维子空间，对应于格拉斯曼流形$\text{Gr}(2, r)$Gr(2,r)上的一个点。该子空间通过普吕克坐标编码，这些坐标源自两个向量的外积。具体而言，普吕克向量$p_t^{(\Delta)} \in \mathbb{R}^{\binom{r}{2}}$pt(Δ)​∈R(2r​)计算为$p_{ij}^{(\Delta)}(t) = z_{t,i} z_{t+\Delta,j} - z_{t,j} z_{t+\Delta,i}$pij(Δ)​(t)=zt,i​zt+Δ,j​−zt,j​zt+Δ,i​，其中$1 \leq i < j \leq r$1≤i<j≤r。这些坐标在有限维射影空间中表示该对的局部几何结构，满足已知的代数约束。

随后，普吕克向量通过学习的线性映射$g_t^{(\Delta)} = W_{\text{plü}} \hat{p}_t^{(\Delta)} + b_{\text{plü}}$gt(Δ)​=Wplu¨​p^​t(Δ)​+bplu¨​投影回模型原始维度，其中$\hat{p}_t^{(\Delta)}$p^​t(Δ)​是普吕克向量的归一化版本，以保证数值稳定性。在每个位置$t$t上，对所有有效偏移的特征进行聚合，形成单一几何特征向量$g_t$gt​。该向量捕捉多尺度局部几何，并通过门控机制与原始隐藏状态$h_t$ht​融合。门控值$\alpha_t$αt​计算为$\sigma(W_{\text{gate}} [h_t; g_t] + b_{\text{gate}})$σ(Wgate​[ht​;gt​]+bgate​)，混合表示为$\tilde{h}_t^{\text{mix}} = \alpha_t \odot h_t + (1 - \alpha_t) \odot g_t$h~tmix​=αt​⊙ht​+(1−αt​)⊙gt​。该融合步骤使模型能够自适应地结合原始表示与几何特征。

门控融合后，表示经过层归一化和dropout处理。一个位置前馈网络（由两个线性层、GELU非线性及残差连接组成）进一步处理隐藏状态。该模块的输出经过归一化，作为下一层的更新隐藏状态。整个过程在$N$N层中重复，构成完整的因果格拉斯曼Transformer。

与标准自注意力的关键区别在于，不存在$L \times L$L×L注意力矩阵及其相关的二次复杂度。模型不再在所有词元位置间计算成对兼容性得分，而是作用于具有受控自由度的有限维流形。格拉斯曼混合层的复杂度在固定秩$r$r和窗口大小$m$m下与序列长度呈线性关系，而全自注意力则呈二次增长。这种线性增长源于前馈网络和线性操作的主导项$O(Ld^2)$O(Ld2)，而普吕克计算与投影贡献$O(Lmr^2)$O(Lmr2)，在固定$r$r和$m$m下为次主导项。作者认为，从张量提升转向几何流的转变，为序列建模提供了更具可解释性和解析可处理性的基础，因为模型行为的演化可被研究为在明确定义流形上的轨迹，而非高维、无结构张量的复合。

实验

• 在Wikitext-2语言建模任务上，GrassmannLM在6层模型上达到275.7的验证困惑度，在12层模型上达到261.1，尽管未使用任何注意力，仍保持与同规模TransformerLM相差10–15%以内，且深度越大差距越小。
• 在以DistilBERT为骨干的SNLI自然语言推理任务上，Grassmann-Plücker头达到85.50的验证准确率和85.38的测试准确率，略优于Transformer头（85.45验证，85.11测试）。
• Grassmann架构证明了其作为无注意力序列模型的可行性，参数量相近且在各类设置下表现一致，验证了几何结构化的局部混合可支持语义推理。
• 实验运行时间仍慢于Transformer基线，因实现未优化，但理论复杂度与序列长度呈线性关系，表明未来通过专用优化具备显著扩展潜力。

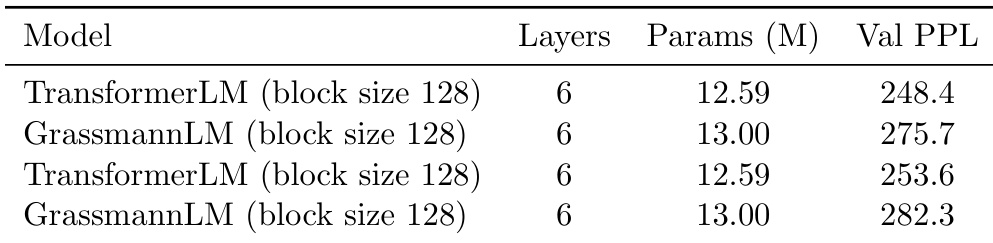
作者使用表格在相同条件下比较TransformerLM与GrassmannLM在Wikitext-2语言建模任务上的表现。结果显示，GrassmannLM的验证困惑度高于TransformerLM，分别为275.7和282.3，而TransformerLM为248.4和253.6，表明尽管参数略多，Grassmann模型表现更差。

作者使用块大小为256的12层模型比较TransformerLM与GrassmannLM在语言建模上的表现。结果显示，GrassmannLM的验证困惑度为261.1，高于TransformerLM的235.2，表明在此条件下存在性能差距。

作者使用DistilBERT骨干网络，搭配两种不同分类头——Transformer头与Grassmann-Plücker头，评估其在SNLI自然语言推理任务上的表现。结果显示，Grassmann-Plücker头在验证和测试准确率上均略高于Transformer头，表明分类头中显式的几何结构可提升下游推理任务的性能。