One-sentence Summary

The authors from Hong Kong University of Science and Technology propose LanPaint, a training-free, asymptotically exact method for partial conditional sampling in ODE-based and rectified-flow diffusion models, leveraging efficient Langevin dynamics to enable backpropagation-free, Monte Carlo inference with precise distributional matching and high-quality inpainting, outperforming prior approaches in speed and visual coherence.

Key Contributions

• Existing training-free methods for partial conditional sampling in diffusion models face fundamental limitations, including intractable inverse formulations, reliance on heuristic losses or backpropagation, and incompatibility with fast ODE-based samplers, leading to poor distributional matching and inefficient inference.
• LanPaint introduces a training-free, asymptotically exact approach using carefully designed Langevin dynamics, featuring a bidirectional guided score for mutual adaptation between known and inpainted regions and a fast Langevin dynamics scheme enabling high-fidelity sampling in just 5 inner iterations per step.
• Experiments on diverse models—including HiDream, Flux, SD 3.5, and SD XL—demonstrate superior inpainting quality and visual coherence, with results achieved via ODE-based samplers and without gradient computation, validating its efficiency and compatibility with modern diffusion architectures.

Introduction

Diffusion models have become dominant in image generation, particularly through efficient ODE-based and rectified flow samplers that enable fast, deterministic sampling. However, their standard denoising mechanism struggles with training-free partial conditional sampling—such as inpainting with known pixels—because existing methods either rely on computationally expensive stochastic sampling, heuristic loss functions that fail to match the true conditional distribution, or suffer from convergence issues and local minima traps. Prior approaches are often incompatible with fast ODE solvers or require model-specific training, limiting their generality and practicality. The authors introduce LanPaint, a training-free method that achieves asymptotically exact partial conditional sampling by leveraging a novel bidirectional guided score and a fast Langevin dynamics scheme. This enables high-fidelity inpainting with just five inner iterations per step, compatibility with ODE and rectified flow samplers, and backpropagation-free inference—overcoming key limitations of prior work while maintaining strong performance across diverse diffusion architectures.

Method

The authors leverage a diffusion model framework to address the challenge of partial conditional sampling, particularly for image inpainting tasks. The core of the method is built upon the Denoising Diffusion Probabilistic Model (DDPM), which models a joint distribution $p(\mathbf{z}) = p(\mathbf{x}, \mathbf{y})$p(z)=p(x,y) over an image $\mathbf{z}$z, where $\mathbf{x}$x is the region to be inpainted and $\mathbf{y}$y is the observed region. The model is trained to reconstruct a clean image $\mathbf{z}_0$z0​ from progressively noisier versions, using a forward diffusion process that gradually adds Gaussian noise to the data. This process is governed by an Ornstein–Uhlenbeck (OU) stochastic differential equation (SDE), which transitions the data distribution $p(\mathbf{z})$p(z) to a pure Gaussian noise distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$N(0,I). To sample from the learned distribution, the model reverses this process. The backward diffusion is formulated as an SDE or an ordinary differential equation (ODE), where the score function $\mathbf{s}(\mathbf{z}, t) = \nabla_{\mathbf{z}} \log p_t(\mathbf{z})$s(z,t)=∇z​logpt​(z) guides the removal of noise. This score function is typically learned by a neural network, such as a U-Net, which is trained to predict the noise added at each step of the forward process.

[[IMG:|Figure 2: Comparison of inpainting methods for conditional distribution sampling (known y, inpaint x). Left: Ground truth Gaussian samples. Middle: KL divergence versus diffusion steps across methods ("-10" denotes 10 inner iterations where applicable). Right: Effect of inner iterations at 20 diffusion steps. The dashed line at KL=0.01 highlights the performance gap between asymptotically exact methods and heuristic approaches.]]

The primary challenge in inpainting is that the conditional score function $\mathbf{s}_{\mathbf{x}|\mathbf{y}_o} = \nabla_{\mathbf{x}} \log p_t(\mathbf{x}|\mathbf{y}_o)$sx∣yo​​=∇x​logpt​(x∣yo​), which is required for direct sampling, is inaccessible. To overcome this, the authors propose a decoupling approximation, $q_t(\mathbf{x}, \mathbf{y}|\mathbf{y}_o) = p_t(\mathbf{x}|\mathbf{y}) \cdot p_t(\mathbf{y}|\mathbf{y}_o)$qt​(x,y∣yo​)=pt​(x∣y)⋅pt​(y∣yo​), which approximates the true conditional distribution. This approximation is tractable because $p_t(\mathbf{y}|\mathbf{y}_o)$pt​(y∣yo​) is analytically known from the forward process, and $p_t(\mathbf{x}|\mathbf{y})$pt​(x∣y) shares the same score as the joint distribution. The authors then introduce a novel method, Bidirectional Guided (BiG) Score, to generate samples from this approximate distribution. The BiG score, $\mathbf{g}_{\lambda}(\mathbf{x}, \mathbf{y}, t)$gλ​(x,y,t), is designed to enable bidirectional feedback between the inpainted region $\mathbf{x}_t$xt​ and the observed region $\mathbf{y}_t$yt​. It is derived by incorporating information from $\mathbf{x}_t$xt​ into the sampling of $\mathbf{y}_t$yt​, while preserving the observed content. The BiG score is defined as a combination of the score of the conditional distribution $p_t(\mathbf{y}|\mathbf{y}_o)$pt​(y∣yo​) and the score of the joint distribution $p_t(\mathbf{y}|\mathbf{x})$pt​(y∣x), with a guidance scale $\lambda$λ that controls the strength of the feedback. This allows the model to escape local optima that can trap the inpainted region in prior methods.

[[IMG:|Figure 9: We analyze the average norm ratio between the ideal score $\mathbf{s}_{\mathbf{y}}^{*}$sy∗​ (Eq.65) and the component discarded by the BiG score, $\mathbf{s}_{\mathbf{y}}^{*}-\mathbf{g}_{\lambda}$sy∗​−gλ​, relative to $\bar{\\alpha}_{t}$alphaˉ​t​, in the conditional Gaussian case (Section 5.1). We focus on the right part of the image when $\bar{\\alpha}_{t}$alphaˉ​t​ approaches 1 (i.e., $t \\rightarrow 0$trightarrow0), which determines the distribution of generated clean image. This ratio decreases at the same rate as $\\sqrt{1-\\bar{\\alpha}_{t}}$sqrt1−baralphat​, indicating that the BiG score $\mathbf{g}_{\lambda}$gλ​ closely approximates the ideal score $\mathbf{s}_{\mathbf{y}}^{*}$sy∗​ with negligible error as $t \\rightarrow 0$trightarrow0. This confirms that the error scales as $\\mathcal{O}(\\sqrt{1-\\bar{\\alpha}_{t}})$mathcalO(sqrt1−baralphat​), laying the foundation for Theorem 4.1.]]

To efficiently sample from the distribution defined by the BiG score, the authors propose Fast Langevin Dynamics (FLD), a variant of Underdamped Langevin Dynamics (ULD). FLD introduces a momentum variable $\mathbf{q}_{\tau}$qτ​ into the Langevin dynamics, which acts as a time-averaged force, accelerating convergence to the stationary distribution. The dynamics are defined by a system of SDEs for the state $\mathbf{z}_{\tau} = (\mathbf{x}_{\tau}, \mathbf{y}_{\tau})$zτ​=(xτ​,yτ​) and its momentum $\mathbf{q}_{\tau}$qτ​. A key innovation is the use of a diffusion damping force in the numerical solver. This force is derived from the forward diffusion process and ensures that the solution remains stable, even for large time steps. The FLD solver is an analytical solution to the dynamics, which treats the score function as constant over a time interval, and is designed to preserve the stationary distribution of the original Langevin dynamics. The method is further enhanced by a parameter schedule that maintains a constant discriminant, ensuring consistent damping behavior throughout the diffusion process. This allows for stable and efficient sampling with larger step sizes, overcoming the trade-off between convergence speed and numerical stability inherent in standard Langevin dynamics.

Experiment

• LanPaint validates exact conditional sampling on a 2D synthetic Gaussian benchmark, achieving near-zero KL divergence with fewer diffusion and inner iteration steps than TFG, FLD, and heuristic methods (MCG, DPS, CoPaint, DDRM), which fail to converge below KL = 0.01.
• On a 500-component Gaussian mixture distribution, LanPaint mitigates local maxima trapping in inpainting, significantly reducing KL divergence compared to baseline methods by leveraging the BiG score to enforce bidirectional information flow between observed and inpainted regions.
• On CelebA-HQ-256 and ImageNet-256, LanPaint achieves state-of-the-art LPIPS and FID scores across diverse mask types (box, half, checkerboard, outpainting) using only 20 Euler steps, outperforming RePaint, TFG, DPS, CoPaint, and MCG, with superior computational efficiency and low memory overhead (599 MB on ImageNet, vs. 5445 MB for backpropagation-based methods).
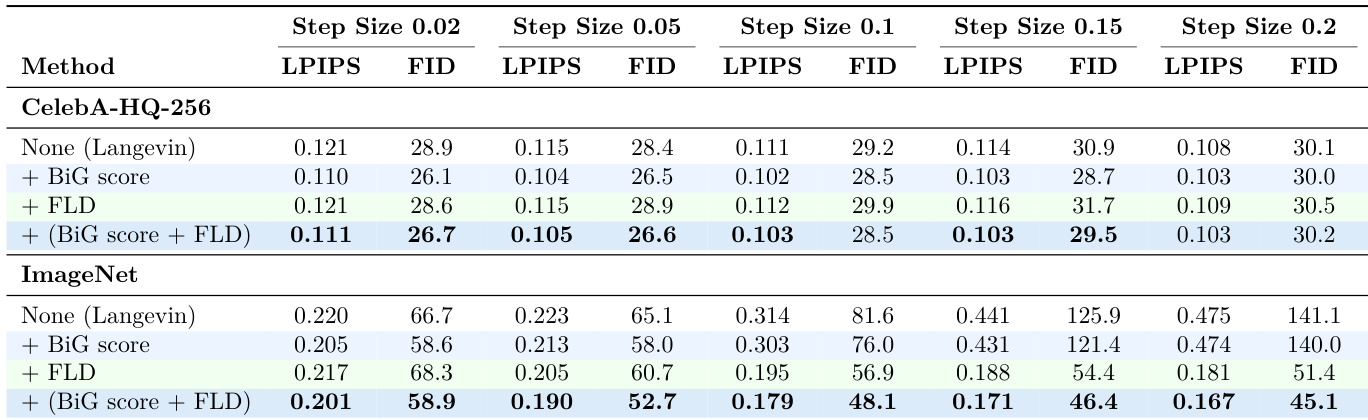
• Ablation studies confirm that both the BiG score and fast Langevin dynamics (FLD) are critical for performance, especially on ImageNet, where FLD enables stable sampling with larger step sizes, while BiG score enhances accuracy across datasets.
• LanPaint demonstrates robust generalization across production-level models—including Stable Diffusion 3.5, Flux.1 Dev, HiDream-L1, and Stable Diffusion XL—on both DDPM and rectified flow architectures, with seamless inpainting and outpainting results validated in ComfyUI.
• LanPaint extends to video inpainting and outpainting on a 14B-parameter T2V model (Wan 2.2), achieving coherent results across 40-frame clips with 20 diffusion steps and two inner iterations, showcasing its dimension-agnostic design.
• LanPaint's performance degrades on distilled models due to reliance on score-based diffusion interpretations, and it assumes noise-free observations, highlighting future research directions in handling noisy inputs and distillation-compatible score learning.

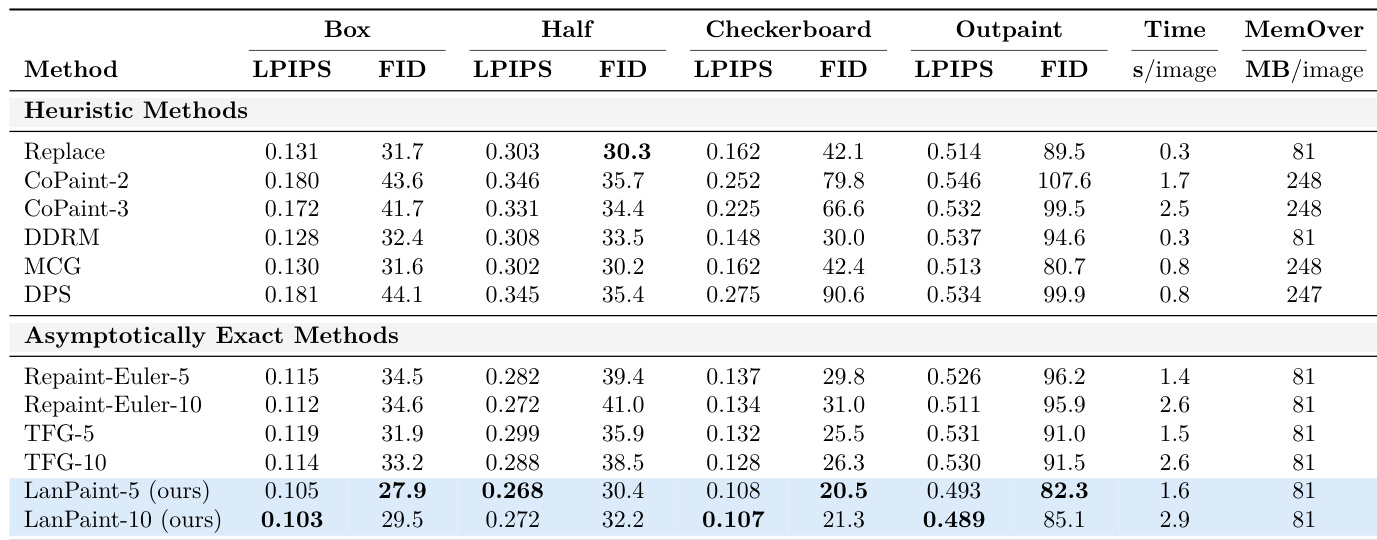
Results show that LanPaint achieves the lowest LPIPS and FID scores across most inpainting tasks, outperforming both heuristic and asymptotically exact methods. The authors use LanPaint-10 to achieve the best overall performance, with significantly lower divergence in checkerboard and outpainting scenarios compared to baselines.

The authors use an ablation study to evaluate the impact of the BiG score and fast Langevin dynamics (FLD) on LanPaint's performance across different step sizes. Results show that on CelebA-HQ-256, the BiG score significantly improves performance while the method remains stable across step sizes, whereas on ImageNet, both components are crucial, with FLD enabling better performance at larger step sizes by preventing divergence.

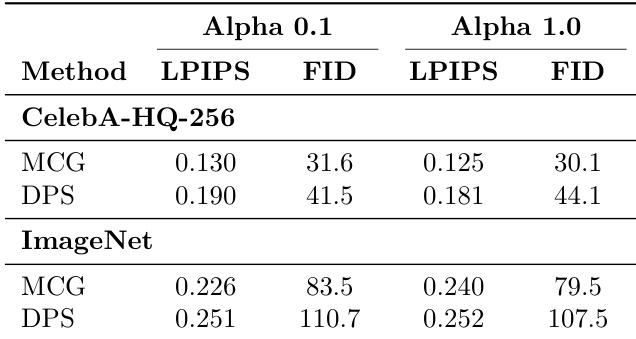
The authors evaluate the impact of different alpha values on MCG and DPS methods in the ablation study. On CelebA-HQ-256, both methods show improved LPIPS and FID scores with alpha 0.1 compared to alpha 1.0, with MCG achieving 0.125 LPIPS and 30.1 FID, and DPS achieving 0.181 LPIPS and 44.1 FID. On ImageNet, MCG and DPS also perform better with alpha 0.1, achieving 0.240 LPIPS and 79.5 FID, and 0.252 LPIPS and 107.5 FID, respectively.

Results show that LanPaint achieves the lowest LPIPS and FID scores across most inpainting and outpainting tasks on CelebA-HQ-256, outperforming both heuristic and asymptotically exact methods. The authors use LanPaint-10 to achieve the best performance, with significantly lower errors compared to baselines, while maintaining competitive computational efficiency.

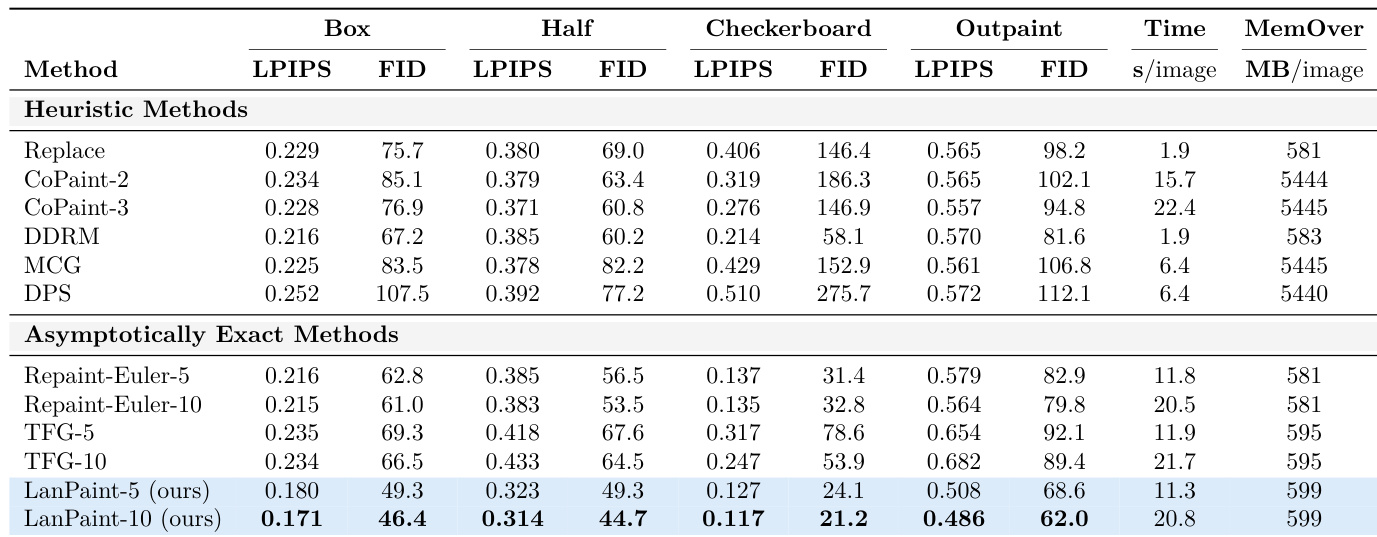
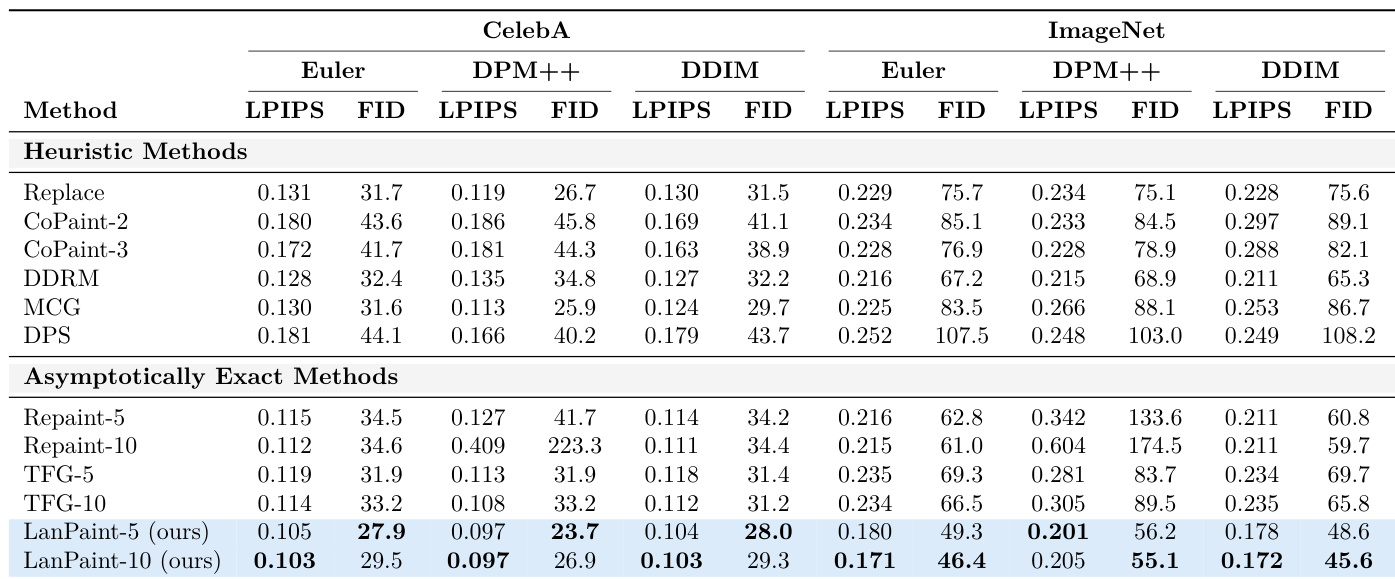
Results show that LanPaint achieves the lowest LPIPS and FID scores across both CelebA and ImageNet datasets, outperforming all heuristic and asymptotically exact methods in most configurations. The authors use the table to demonstrate that LanPaint consistently produces higher quality inpainted images with better perceptual similarity and feature distribution alignment compared to baselines, particularly in challenging tasks like checkerboard and outpainting.