One-sentence Summary

The authors—Moshkov, Hanley, Sorokin, Toshniwal, Henkel, Schifferer, Du, and Gitman—propose a state-of-the-art mathematical reasoning framework that integrates a 540K-item OpenMathReasoning dataset with three core innovations: iterative training for tool-integrated reasoning (TIR) to enable code execution within long CoT chains, a novel generative solution selection (GenSelect) method to identify the best among multiple candidates, and a pipeline for controlling code execution limits. Their OpenMath-Nemotron models achieve top performance on AIMO-2, solving 34 of 50 problems, and are released under a permissive license to advance open-source mathematical AI.

Key Contributions

• We introduce OpenMathReasoning, a large-scale dataset of 540K unique high-quality math problems—including olympiad-level challenges—and 3.2M long-form reasoning solutions, enabling effective distillation and training of open-weight models with strong mathematical reasoning capabilities.

• We develop a novel iterative training pipeline that integrates code execution into long reasoning models through Tool-Integrated Reasoning (TIR), generating 1.7M high-quality solutions by combining instruction-tuned model generation with aggressive quality filtering and controlled execution counts.

• We propose Generative Solution Selection (GenSelect), a method to train models to rank and select the most promising solution from multiple candidates, demonstrating significant improvement over majority voting and enabling higher pass@k performance on mathematical reasoning benchmarks.

Introduction

The authors address the challenge of building high-accuracy mathematical reasoning models for complex, olympiad-level problems, where traditional chain-of-thought methods often fail due to insufficient reasoning depth and lack of executable verification. Prior approaches struggled with limited scale of training data, poor integration of code execution into reasoning flows, and reliance on simple solution aggregation like majority voting, which underperforms relative to theoretical limits. To overcome these limitations, the authors introduce three key innovations: first, they construct OpenMathReasoning, a 540K-problem dataset with 3.2M long-form reasoning solutions, enabling robust distillation of reasoning patterns. Second, they develop a novel iterative pipeline for training models to integrate code execution (Tool-Integrated Reasoning), using quality filtering to refine 1.7M high-fidelity solutions and enabling efficient control over execution count. Third, they propose Generative Solution Selection (GenSelect), a method to train models to rank and select the best solution from multiple candidates, outperforming majority voting. These components are combined into a suite of open-weight models (1.5B to 32B) that support CoT, TIR, and GenSelect inference, achieving state-of-the-art results on AIMO-2, with the winning submission solving 34 of 50 problems. The full dataset, code, and models are released under a permissive license to advance open research.

Dataset

• The dataset is composed of mathematical problems sourced from the Art of Problem Solving (AoPS) community forums, excluding the "Middle School Math" category due to its elementary nature.
• The primary training data is derived from AoPS forum discussions, with a systematic pipeline using Qwen2.5-32B-Instruct for all processing steps.
• Problem extraction identifies and isolates individual problems from forum posts, handling cases with multiple or no problems.
• Each problem is classified into categories: proof-based, multiple-choice, binary (yes/no), or invalid. Multiple-choice, binary, and invalid problems are removed.
• Proof problems are transformed into answer-based questions to align with the model’s expected output format.
• For non-proof problems, the final answer is extracted from forum discussions using LLM-assisted parsing.
• A benchmark decontamination step removes problems closely resembling those in existing math benchmarks, using LLM-based comparison to ensure data freshness.
• The final training dataset is composed of high-quality, non-proof, single-answer problems, with size and composition detailed in Table 1 and Table 2.
• A dedicated validation set, Comp-Math-24-25, is constructed from problems in the 2024 and 2025 American Invitational Mathematics Examinations (AIME) and Harvard-MIT Mathematics Tournaments (HMMT).
• The validation set includes 256 problems, selected for their alignment with AIMO-2 competition standards, covering similar topics and difficulty levels, and excluding proof-based or partial-credit problems.
• The dataset is used in training with a mixture of problem types, where the model is trained on the cleaned AoPS-derived problems and evaluated on the Comp-Math-24-25 benchmark.
• For Chain-of-Thought (CoT) solutions, a subset of 15k samples is generated as stage-0 TIR data, with code execution filtered to retain only solutions containing novel and significant code blocks.
• Code blocks are filtered based on two criteria: whether they perform novel calculations or merely verify prior steps, and whether they contribute significantly to the solution.
• Solutions with incorrect final answers, no code execution, or more than two code blocks are discarded.
• Code block delimiters are standardized during preprocessing: markdown-style "python" and "" tags are replaced with "<tool_call>" and "</tool_call>" to ensure reliable extraction.
• To improve summary quality, native summaries from reasoning models like DeepSeek-R1 are replaced with new summaries generated by Qwen2.5-32B-Instruct.
• Four candidate summaries are generated per solution, up to 2048 tokens, and only those matching the original solution’s answer are retained. The longest valid summary is selected.
• This summary rewriting process is applied to the entire OpenMathReasoning dataset to ensure consistent, informative summaries during inference.

Method

The authors develop a multi-stage pipeline to train models capable of generating high-quality tool-integrated reasoning (TIR) solutions, which combine natural language reasoning with executable Python code. The overall framework begins with a problem input, from which multiple solution summaries are generated. These summaries are categorized into correct and incorrect instances, forming the basis for a generative solution selection (GenSelect) process. The GenSelect pipeline is designed to train a model to select the most promising solution from a set of candidate summaries, thereby improving overall performance beyond simple majority voting.

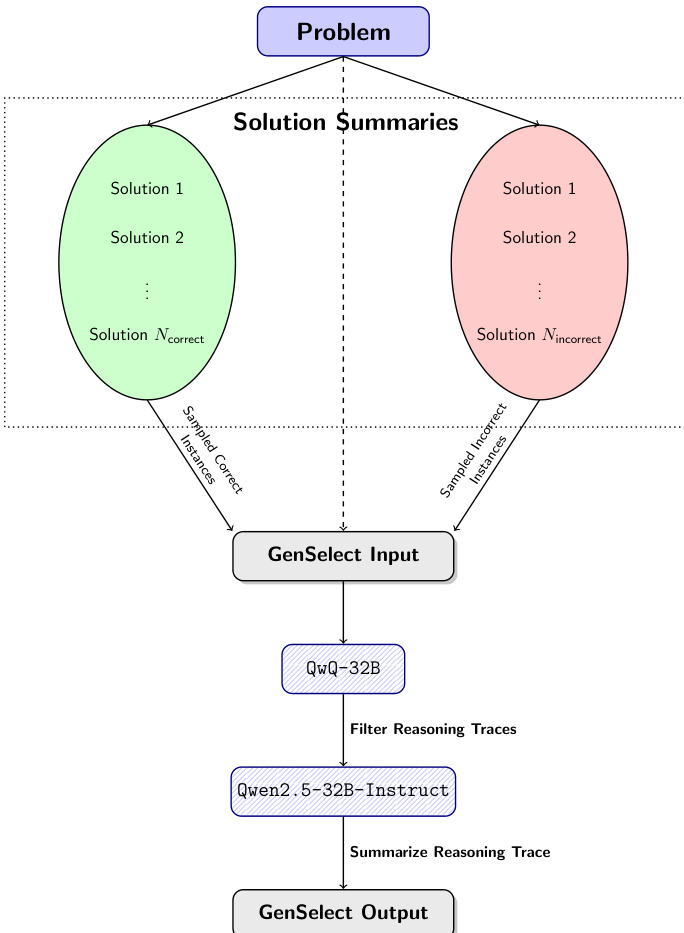
As shown in the figure below, the process starts with a problem, which generates a pool of solution summaries. These summaries are then split into two groups: sampled correct instances and sampled incorrect instances. Both groups are fed into a GenSelect input module, which serves as the basis for training. The QwQ-32B model is used to generate reasoning traces for these inputs, which are then filtered to retain only high-quality reasoning. The filtered traces are passed to a Qwen2.5-32B-Instruct model, which summarizes the reasoning trace into a final GenSelect output. This pipeline enables the model to learn to compare and select the most promising solution from multiple candidates, leveraging natural language reasoning to make the selection. The authors find that this approach significantly improves performance compared to judging each solution in isolation, as it allows the model to reason about the relative quality of different solution paths.

Experiment

• Generated 1.2M CoT solutions using DeepSeek-R1 and QwQ-32B with temperature 0.7, top-p 0.95, and 16384-token limit; filtered to retain only solutions reaching the expected answer via Qwen2.5-32B-Instruct judgment, with ground-truth derived from majority answer across candidates.
• Trained OpenMath-Nemotron series (1.5B to 32B) via supervised fine-tuning on 5.5M samples (3.2M CoT, 1.7M TIR, 566K GenSelect), using RoPE base extension to 500K for longer context; achieved significant CoT accuracy gains with stable TIR performance.
• Applied GenSelect with summarized reasoning traces (capped at 2048 tokens) to reduce inference cost; achieved 1–2% accuracy drop vs. full traces while enabling highly parallelizable pre-filling and efficient inference.
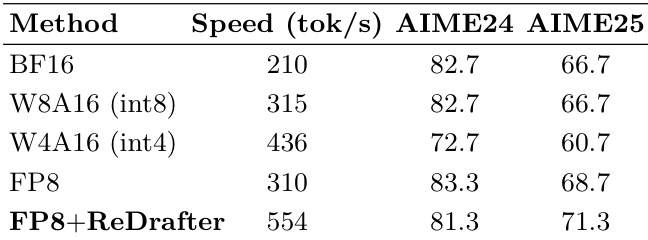
• For Kaggle AIMO-2 submission, merged CoT and TIR checkpoints via linear combination; used speculative decoding with ReDrafter (3-token proposal, 65% acceptance) and time-buffering strategy to meet 5-hour constraint, achieving 34 correct solutions on private leaderboard.
• On Comp-Math-24-25 benchmark, OpenMath-Nemotron-14B (kaggle) achieved pass@1 (maj@64) of 78.4% (85.2%), with 10% longer average generation length than expected, contributing to inference inefficiency despite strong local performance.

Results show that the FP8+ReDrafter method achieves the highest speed at 554 tok/s, while maintaining competitive performance on the AIME24 and AIME25 benchmarks, outperforming other methods in terms of inference efficiency.

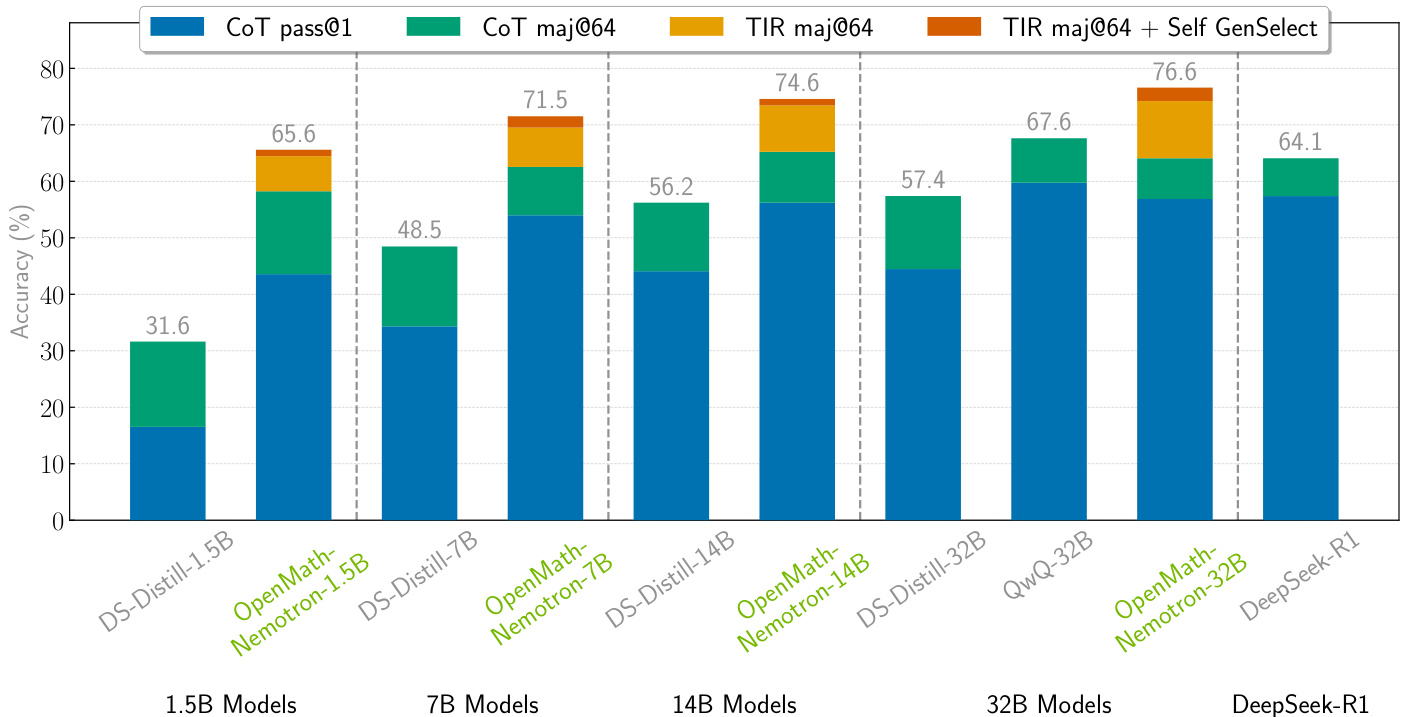
The authors compare the performance of various models on mathematical reasoning tasks, evaluating both CoT and TIR generation methods. Results show that the OpenMath-Nemotron-32B model achieves the highest accuracy with 76.6% on the TIR maj@64 + Self GenSelect setting, significantly outperforming smaller models and other baselines.

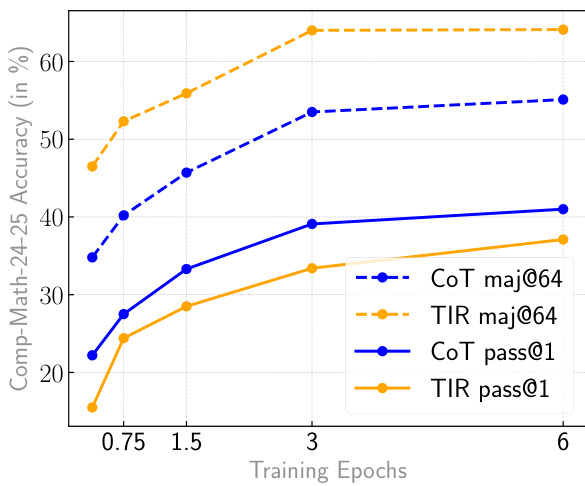
Results show that CoT models achieve higher accuracy than TIR models across all training epochs, with CoT maj@64 and CoT pass@1 consistently outperforming their TIR counterparts. The accuracy of both model types increases with training epochs, but CoT models demonstrate a more significant improvement, particularly in the majority voting setting.

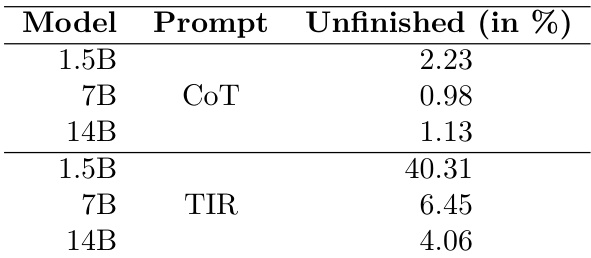
Results show that the TIR prompt leads to significantly higher rates of unfinished solutions compared to the CoT prompt across all model sizes, with the 1.5B model exhibiting the most pronounced difference. The authors hypothesize that smaller models are less consistent in using tools effectively, which contributes to the higher rate of incomplete solutions when using the TIR prompt.

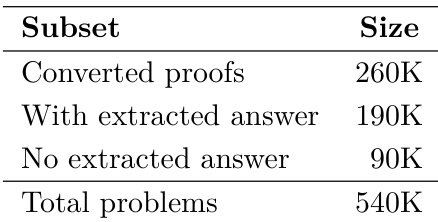
The authors present a dataset of 540K math problems, categorized into three subsets: 260K converted proofs, 190K with extracted answers, and 90K without extracted answers. This distribution reflects the different stages of solution processing and data availability in their dataset construction.