One-sentence Summary

The author, affiliated with the University of Michigan, proposes a novel quasi-Newton method based on the parameterization framework to directly compute subharmonic periodic orbits (SPOs) and their Floquet vectors and multipliers in perturbed 4D symplectic maps, enabling efficient continuation in ε and Taylor parameterization of associated weak manifolds—offering significant improvements over multi-shooting methods and demonstrating utility in modeling resonant orbits within 2.5 DOF Hamiltonian systems, such as those arising in celestial mechanics.

Key Contributions

• This paper addresses the challenge of computing long, unstable subharmonic periodic orbits (SPOs) in perturbed 2.5 degree-of-freedom Hamiltonian systems—such as stroboscopic maps of periodically perturbed 2 DOF flows—where these orbits arise from resonant tori in the unperturbed system and are critical for understanding the breakdown of invariant tori via resonance overlap.

• The authors introduce a novel quasi-Newton method that simultaneously computes SPOs, their Floquet multipliers, and Floquet vectors by adapting the parameterization method framework to periodic orbits, enabling efficient continuation in the perturbation parameter ε while avoiding the costly $O(q^3)$O(q3) linear solves typical of traditional multiple-shooting approaches.

• The method is demonstrated on real celestial mechanics problems, including resonant orbits in the Jupiter-Europa-Ganymede system, and enables the subsequent computation of Taylor parameterizations for the weak stable and unstable manifolds of these SPOs, providing a powerful tool for studying global dynamics in high-dimensional symplectic systems.

Introduction

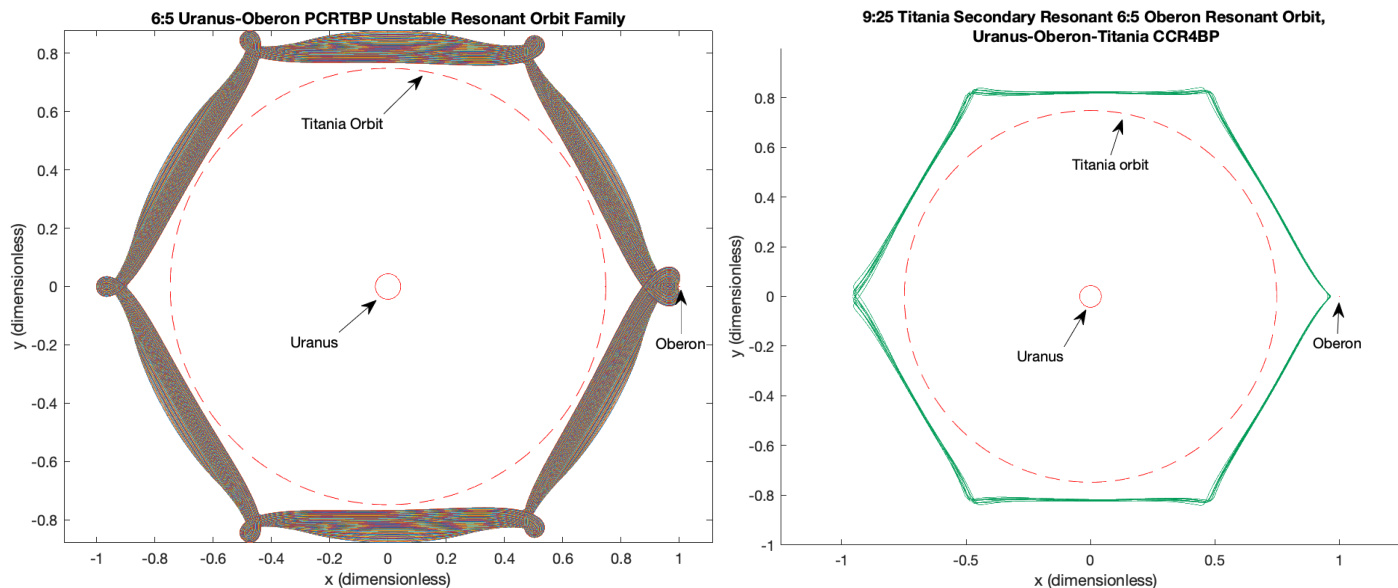
The authors address the challenge of computing long, unstable periodic orbits—known as subharmonic periodic orbits (SPOs)—in 4D symplectic maps that arise from periodically perturbed 2 DOF Hamiltonian systems, such as the planar circular restricted 4-body problem in celestial mechanics. These orbits are critical for understanding the breakdown of invariant tori due to secondary resonances, especially when perturbations cause separatrices from long-period orbits to intersect, leading to chaotic dynamics. Prior methods rely on multiple-shooting algorithms that require solving large $4q \times 4q$4q×4q linear systems to find both the orbit points and their stability properties, resulting in $O(q^3)$O(q3) computational complexity—prohibitive for large $q$q. The authors’ main contribution is a novel fast multiple-shooting method that simultaneously computes SPOs and their Floquet vectors and multipliers by adapting the parameterization method to periodic orbits. This approach avoids solving large linear systems by embedding the Floquet equations directly into the Newton iteration, reducing computational cost and enabling direct access to stability information. The method is applicable to a broad class of 4D symplectic maps and has been successfully applied to compute SPOs and their separatrices in real-world models of the Jupiter-Europa-Ganymede and Uranian systems, demonstrating its utility in space mission design and dynamical systems analysis.

Method

The authors develop a quasi-Newton method for the simultaneous computation of subharmonic periodic orbits (SPOs) and their associated Floquet vectors and multipliers within a family of 4D symplectic maps $F_\varepsilon$Fε​. This framework is designed to study the persistence of SPOs from an unperturbed map $F_0$F0​ into a perturbed system, enabling numerical continuation with respect to the perturbation parameter $\varepsilon$ε. The method is an adaptation of the parameterization method for invariant tori, but is uniquely tailored to compute periodic orbits directly. The core of the algorithm involves solving a system of equations for the SPO points $X_\varepsilon(k)$Xε​(k), $k=0,\ldots,q-1$k=0,…,q−1, and the matrices $P_\varepsilon(k)$Pε​(k) and $\Lambda_\varepsilon(k)$Λε​(k) that represent the Floquet vectors and multipliers. The invariance equation for the SPO is $F_\varepsilon(X_\varepsilon(k)) = X_\varepsilon(k+1 \mod q)$Fε​(Xε​(k))=Xε​(k+1modq), while the Floquet equation is $DF_\varepsilon(X_\varepsilon(k))P_\varepsilon(k) = P_\varepsilon(k+1 \mod q)\Lambda_\varepsilon(k)$DFε​(Xε​(k))Pε​(k)=Pε​(k+1modq)Λε​(k). The matrix $\Lambda_\varepsilon(k)$Λε​(k) is constrained to a near-diagonal form, with the stable and unstable multipliers $\lambda_s(k)$λs​(k) and $\lambda_u(k)$λu​(k) on the diagonal, and the internal dynamics multipliers $\lambda_1$λ1​ and $\lambda_2$λ2​ in the top-left block, which may include an off-diagonal term $T$T. This structure allows the system of equations to be decoupled into a series of 1D linear problems, which are solved efficiently using fixed-point iteration or explicit formulas, depending on the spectral properties of the multipliers. The method proceeds by first initializing the solution for $\varepsilon=0$ε=0 using the known unperturbed SPO and its monodromy matrix, and then numerically continuing this solution to $\varepsilon>0$ε>0 through a series of quasi-Newton steps. Each step involves correcting the SPO points $X$X and the Floquet matrices $P$P and $\Lambda$Λ to reduce the residual errors $E(k)$E(k) and $E_{red}(k)$Ered​(k), which measure the violation of the invariance and Floquet equations, respectively. The correction for $X$X is derived from a linearized equation for the correction vector $\xi(k)$ξ(k), while the correction for $P$P and $\Lambda$Λ is derived from a similar equation for $Q(k)$Q(k) and $\Delta\Lambda(k)$ΔΛ(k). After each correction, a Schur decomposition is applied to the updated $\Lambda_c(k)$Λc​(k) to ensure it maintains the required near-diagonal form, which is crucial for numerical stability. The resulting SPO and Floquet vectors are then used to compute Taylor parameterizations of the SPO's weak stable and unstable manifolds, if they exist.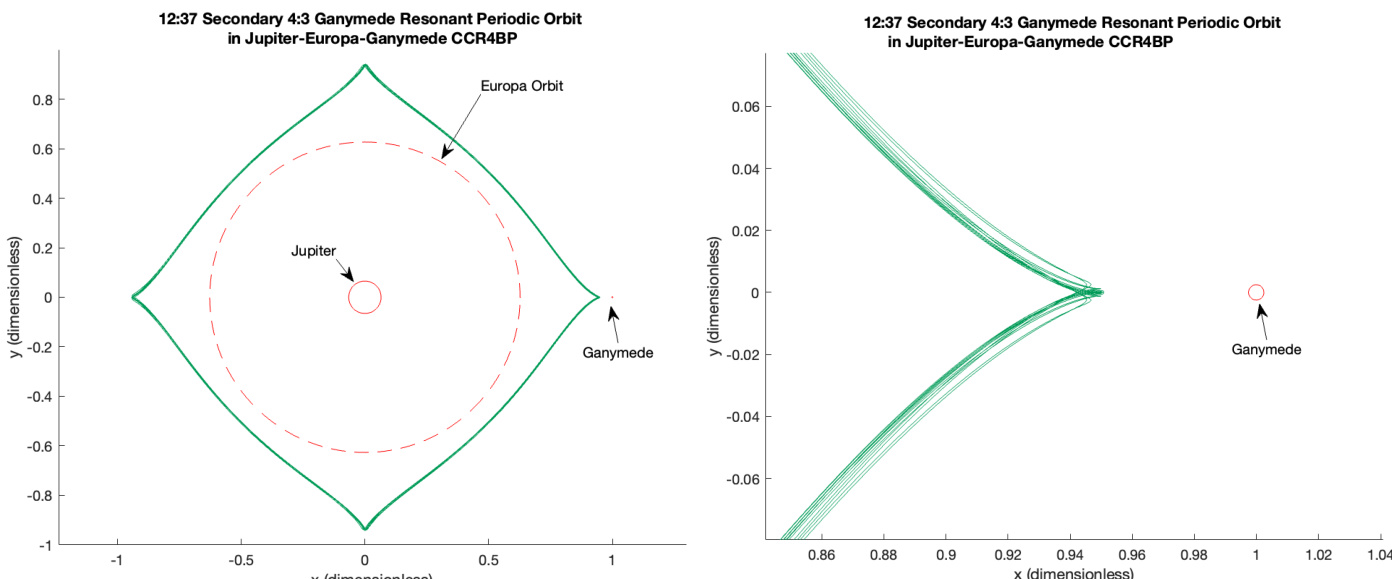

Experiment

• Computed secondary resonant periodic orbits (SPOs) and their separatrices in the CCR4BP models of Jupiter-Europa-Ganymede and Uranus-Titania-Oberon systems using numerical continuation and the parameterization method.
• Successfully continued SPOs with frequency ratios ω/(2π) = 11/34, 34/105, 23/71, 35/108, 12/37, 25/77, 37/114, and 45/139 in the Jupiter-Europa-Ganymede CCR4BP (ε = 2.5265 × 10⁻⁵), where invariant tori failed to persist due to resonance overlap.
• Detected intersections of separatrices from consecutive SPOs in both systems, confirming the dynamical mechanism of torus destruction in regions with ω < 2.04047 (Jovian) and similar low-frequency ranges (Uranian).
• Achieved accurate computation of separatrices using the parameterization method with Floquet directions, enabling visualization of nonlinear structures in action-angle-like coordinates.
• All computations performed in Julia with OrdinaryDiffEq.jl, TaylorSeries.jl, and TaylorIntegration.jl; numerical integration used DP8 adaptive step size method; SPOs computed with 10⁻⁷ tolerance and step sizes Δε = 5 × 10⁻⁷ to 10⁻⁶.